“Mathematics requires a small dose, not of genius, but of an imaginative freedom which, in a larger dose, would be insanity. And if mathematicians tend to burn out early in their careers, it is probably because life has forced them to acquire too much common sense, thereby rendering them too sane to work. But by then they are sane enough to teach, so a use can still be found for them.”
Angus K. Rodgers
For this week, I’ll write about the theory of root systems, especially things related to Weyl groups, weight spaces and etc, for the purpose of my URA. This is because one of the objectives of my URA is to generalise my previous blog post about a fraction of an \(S_n\)-orbit on a hyperplane to Weyl groups. First, a Lie algebra is simple if it is of degree greater than \(1\) (so we are excluding the one dimensional abelian Lie algebras) and has no proper ideals, and a semisimple Lie algebra is a direct sum of simple Lie algebras. Equivalently, a Lie algebra \(\mathfrak{g}\) is semisimple if \(\mathrm{rad}(\mathfrak{g})\), the sum of all solvable ideals (or the maximal solvable ideal), is trivial. Any semisimple Lie algebra \(\mathfrak{g}\) is the Lie algebra of an algebraic group \(G\). Let \(\mathrm{ad}:\mathfrak{g}\rightarrow \mathfrak{gl}(\mathfrak{g})\) by \((\mathrm{ad} X)(Z)=[X,Z]\) be the adjoint representation. Let \(B:\mathfrak{g}\times \mathfrak{g}\rightarrow \mathbf C\) be the symmetric bilinear form defined by \(B(X,Y)=\mathrm{tr}(\mathrm{ad}X\mathrm{ad} Y)\), called the Killing form which is invariant in the sense of \(B([X,Y],Z)=B(X,[Y,Z])\). Cartan’s criterion for semisimplicity says that a Lie algebra is semisimple iff the associated Killing form is nondegenerate. From now on, we let \(\mathfrak{g}\) be a semisimple Lie algebra over \(\mathbf C\). We start by discussing the root–space decomposition \(\mathfrak{g}=\mathfrak{h}\oplus \bigoplus_{\alpha\in\Phi}\mathfrak{g}_{\alpha}\) of semisimple Lie algebras.
Root–space decomposition
Before we begin, we review some terminology. We say that \(\mathfrak{g}\) is abelian if the Lie bracket is identically zero, and a subspace \(\mathfrak{i}\) is an ideal if \([X,Y]\in\mathfrak{i}\) for all \(X\in \mathfrak{g}\) and \(Y\in\mathfrak{i}\). Examples include \(Z(\mathfrak{g})=\{Z\in\mathfrak{g}:[X,Z]=0,\forall X\in\mathfrak{g}\}\) called the center, \(N_{\mathfrak{g}}(k)=\{X\in\mathfrak{g}:[X,K]\in k,\,\forall K\in k\}\) called the normaliser where \(k\) is a subspace of \(\mathfrak g\), and \(C_{\mathfrak g}(k)=\{X\in\mathfrak{g}:[X,K]=0,\,\forall K\in k\}\) called the centraliser where \(k\) is a subset of \(\mathfrak g\). For ideals \(\mathfrak{i},\mathfrak{j}\) of \(\mathfrak{g}\), define \([\mathfrak{i},\mathfrak{j}]\) to be the ideal spanned by \([X,Y]\) where \(X\in \mathfrak{i},Y\in \mathfrak{j}\). We say \(\mathfrak{g}\) is nilpotent if the chain \(\mathfrak{g}\ge [\mathfrak{g},\mathfrak{g}]\ge [\mathfrak{g},[\mathfrak{g},\mathfrak{g}]]\ge \cdots\) called the lower central series terminates in zero. We say \(\mathfrak{g}\) is solvable if the chain \(\mathfrak{g}\ge [\mathfrak{g},\mathfrak{g}]\ge [[\mathfrak{g},\mathfrak{g}],[\mathfrak{g},\mathfrak{g}]]\ge \cdots\) called the derived series terminates in zero. We say \(X\in\mathfrak{g}\) is ad-nilpotent if \(\mathrm{ad}X\) is a nilpotent endomorphism, and semisimple if \(\mathrm{ad}X\) is diagonalisable.
Definition 1. A subalgebra \(\mathfrak{h}\) of \(\mathfrak{g}\) is Cartan if \(\mathfrak h\) satisfies one of the equivalent conditions
- nilpotent and self-normalising (\(N_\mathfrak{g}(\mathfrak h)=\mathfrak h\))
- (if \(\mathfrak g\) is f.d. over field of char. 0) a maximal subalgebra consisting of semisimple elements,
A Cartan subalgebra \(\mathfrak{h}\) is abelian, and combine this with the fact that all elements are semisimple, we have \(\mathrm{ad}[\mathfrak h]\) are simultaneously diagonalisable and there is a direct sum decomposition \(\mathfrak{g}=\bigoplus_{\alpha\in \mathfrak h^*}\mathfrak g_{\alpha}\) where \(\mathfrak{h}^*\) is the dual space and \(\mathfrak{g}_{\alpha}=\{X\in\mathfrak g: (\mathrm{ad}H)(X)=\alpha (H)X,\forall H\in\mathfrak h\}\). We have \(\mathfrak g_0=\mathfrak h=C_{\mathfrak g}(\mathfrak h)\). Let \(\Phi=\{\alpha\in \mathfrak{h}^*: \alpha\ne 0, \mathfrak g_{\alpha}\ne 0\}\),
\[\mathfrak g=\mathfrak h\oplus\bigoplus_{\alpha\in\Phi}\mathfrak g_{\alpha}\]The elements of \(\Phi\) are called roots, which there are only finitely many. The spaces \(\mathfrak g_{\alpha}\) with \(\alpha\) a root is called the root spaces. It turns out that root spaces all have dimension \(1\).
Example 2. Let \(E_{i,j}\) be the matrix with \(1\) at \((i,j)\) and \(0\) elsewhere.
- Suppose \(\mathfrak g=\mathfrak{sl}_n(\mathbf C)=\{M\in\mathrm{Mat}_n(\mathbf C): \mathrm{tr}(M)=0\}\). We have the Cartan subalgebra \(\mathfrak h\) consists of all diagonal matrices. Let \(e_i\in\mathfrak h^*\) output the \(i\)-th diagonal, then \(\mathrm{ad}(H)E_{i,j}=(e_i(H)-e_j(H))(E_{i,j})\). Thus the roots are \(\alpha_{i,j}=e_{i}-e_{j}\) for \(i\ne j\) and the corresponding root spaces are \(\mathbf CE_{i,j}\).
- Suppose \(\mathfrak g=\mathfrak{so}_{2n+1}(\mathbf C)=\{M\in\mathrm{Mat}_{2n+1}(\mathbf C): M^{\mathrm T}=-M\}\). The Cartan subalgebra \(\mathfrak h\) consists of the block diagonal matrices with a \(1\)-by-\(1\) zero block and \(n\) \(2\)-by \(2\) blocks of the form
\[\begin{pmatrix}0 & ih_j\\ -ih_j & 0\end{pmatrix}\]Let \(e_j\in\mathfrak h^*\) output \(h_j\). The roots are \(\pm e_i\pm e_j\) for \(i\ne j\) and \(e_k\) for \(k\). The root spaces are in Knapp II.1.- Suppose \(\mathfrak{g}=\mathfrak{sp}_{2n}(\mathbf C)=\{M\in\mathrm{Mat}_{2n}(\mathbf C): M^\mathrm{T}J=-JM\}\) where
\[J=\begin{bmatrix}\mathbf{0} & I\\ -I& \mathbf{0}\end{bmatrix}\]The Cartan subalgebra \(\mathfrak h\) consists of the diagonal matrices of the form
\[\begin{bmatrix}H & \mathbf{0} \\ \mathbf{0} & -H\end{bmatrix}\]where \(H\in\mathrm{Mat}_n(\mathbf C)\) is diagonal. Let \(e_j\in\mathfrak{h}^*\) output the the \(j\)-th diagonal of \(H\) in the above matrix. The roots are \(\pm e_i\pm e_j\) for \(i\ne j\) and \(\pm 2e_k\) for \(k\). The root spaces are in Knapp II.1.- Suppose \(\mathfrak g=\mathfrak{so}_{2n}(\mathbf C)=\{M\in\mathrm{Mat}_{2n}(\mathbf C): M^{\mathrm T}=-M\}\). The Cartan subalgebra is similar to that of \(\mathfrak g=\mathfrak{so}_{2n}(\mathbf C)\) except the last zero block. The roots are \(\pm e_i\pm e_j\) with \(i\ne j\).
Note that we have \([\mathfrak g_{\alpha},\mathfrak{g}_{\beta}]\subseteq \mathfrak{g}_{\alpha+\beta}\), and if \(\alpha,\beta\in\Phi\) and \(\alpha\ne -\beta\) then \(B(\mathfrak g_{\alpha},\mathfrak g_{\beta})=0\). Also, we note that \(\Phi\) spans \(\mathfrak h^*\). In the next section, we define abstract root systems and formalize how we could obtain the Weyl group from \(\Phi\). There is a different way we could define Weyl groups using maximal torus.
Root systems
A root system is a configuration of vectors in the euclidean space that satisfies some geometric properties, which helps us with some classification problems in representation theory of Lie algebras.
Definition 3. A root system is a Euclidean space \(E\) and a finite set of nonzero vectors \(\Phi\subseteq E\) such that
- \(\mathrm{Span}(\Phi)=E\),
- for \(\alpha\in\Phi\), the only scalar multiples of \(\alpha\) in \(\Phi\) are \(\pm \alpha\),
- for any \(\alpha,\beta\in\Phi\), we have \(\langle\beta,\alpha \rangle=2\frac{(\alpha,\beta)}{(\alpha,\alpha)}\in\mathbf Z\) is an integer,
- for \(\alpha\in\Phi\), we have the reflection of any \(\beta\in\Phi\) about the hyperplane perpendicular to \(\alpha\), i.e. \[\sigma_{\alpha}(\beta)=\beta-\langle \beta,\alpha\rangle \alpha=\beta-2\frac{(\alpha,\beta)}{(\alpha,\alpha)}\alpha\]is still in \(\Phi\).
where \((\cdot,\cdot)\) is the standard inner product. The elements of \(\Phi\) are roots. The rank of \(\Phi\) is the dimension of \(E\). A morphism of root systems is a linear morphism between the Euclidean spaces which preserves \(\langle \cdot,\cdot\rangle\). A root system \(\Phi\) is reducible if \(\Phi=\Phi_1\cup\Phi_2\) s.t. \((\alpha,\beta)=0\) for all \(\alpha\in\Phi_1\) and \(\beta\in\Phi_2\).
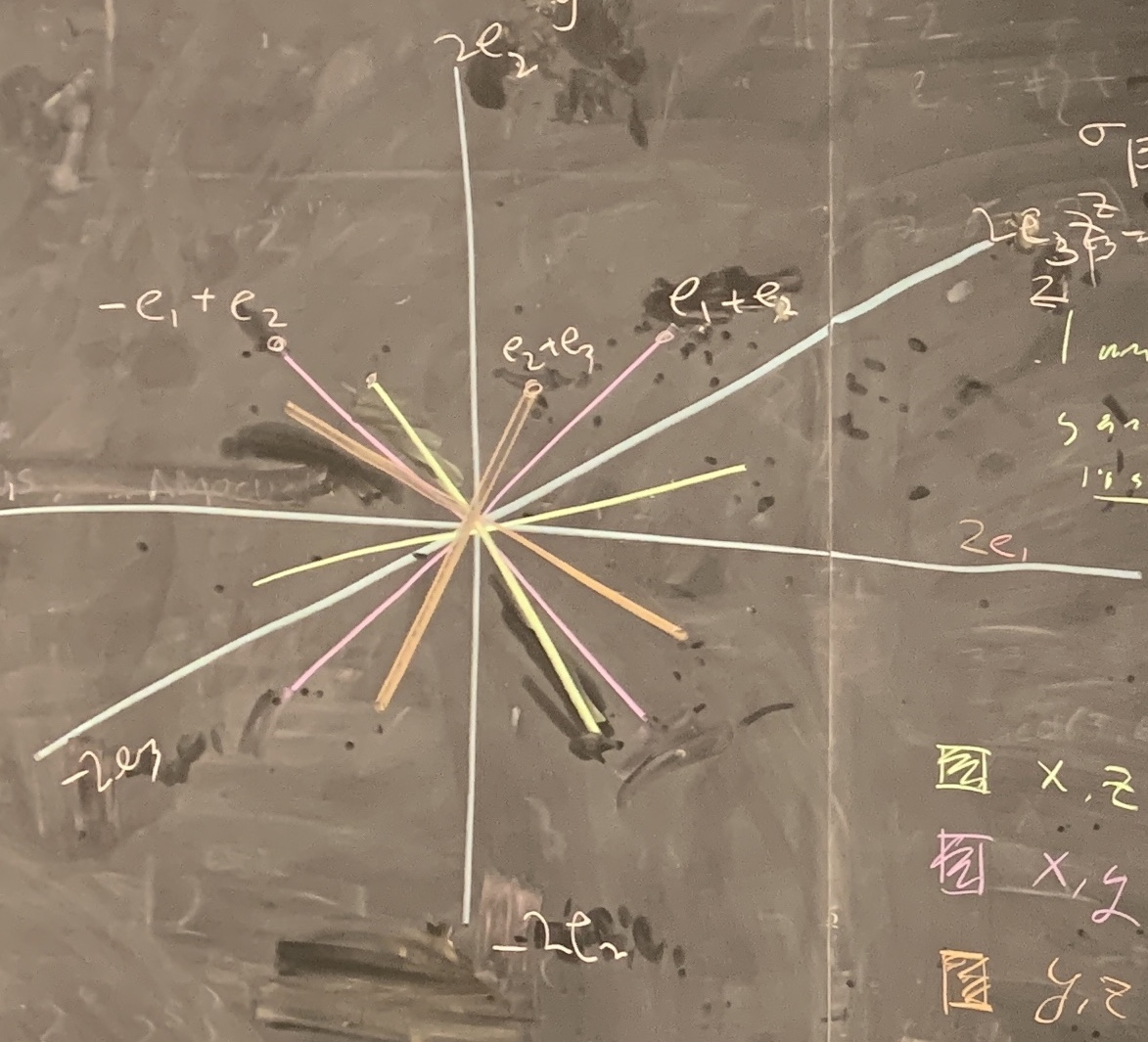
We can draw diagrams of root systems, for example, the following is an example of a root system called \(G_2\). This is in fact an irreducible root system. It does not decompose into disjoint unions that are orthogonal to each other.
I credit this picture to this page of the wikipedia media repository. Here’s another picture of the root system \(C_3\) (arising from the sympletic Lie algebra \(\mathfrak{sp}_{6}\)) drawn by my friend Maya, and a physical model we made together using coffee stirrers (it may not be the most accurate model but it’s hard work).

The Weyl group of a root system \(\Phi\) is the group of all reflections \(W(\Phi)=\{\sigma_{\alpha}:\alpha\in\Phi\}\le \mathrm{GL}(E)\). This is a Coxeter group, i.e. a group with a presentation of the form \(\langle r_1,\dots,r_n\mid (r_ir_j)^{m_{i,j}}\rangle\) where \(m_{i,i}=1\) and \(m_{i,j}>1\) for \(i\ne j\) where \(m_{i,j}=\infty\) when there are no relation. The Weyl group acts faithfully on the roots. For a Lie algebra \(\mathfrak g\) with root space decomposition \(\mathfrak h\oplus \bigoplus_{\alpha\in\Phi}\mathfrak g_{\alpha}\), the set \(\Phi\) is a root system. The Weyl chambers of a root system is the set of connected components of the complement of the union of all hyperplanes perpendicular to a root.
Definition 4. A base for the root system is a subset \(\Delta\subseteq\Phi\), whose elements are called simple roots, such that \(\Delta\) is a basis for \(E\), and each root is a linear combination of \(\Delta\) with integer coefficients such that the coefficients are either all nonnegative or all nonpositive, which are called the positive and negative roots with respect to \(\Delta\). The height of a root with respect to \(\Delta\) is the sum of all its coefficients in the basis \(\Delta\).
Equivalently, we can take a hyperplane not containing any root and define the positive roots as a fixed side, where the simple roots are the positive roots that cannot be written as the sum of two positive roots. The simple roots generate the Weyl group. The fundamental Weyl chamber associated to a base \(\Delta\) is the set of points \(\{v\in E:(\alpha,v)>0,\forall \alpha\in \Delta\}\). For each root \(\alpha\), define the coroot \(\alpha^{\lor}=\frac{2}{\langle \alpha,\alpha\rangle}\alpha\), the set of coroots forms the dual of the root system \(\Phi^\lor\).
Classification of root systems
For \(\alpha,\beta\in\Phi\), since \(\cos(\theta_{\alpha,\beta})=\frac{(\alpha,\beta)^2}{(\alpha,\alpha)(\beta,\beta)}\), we have \(\langle \alpha,\beta\rangle\langle \beta,\alpha\rangle=4\cos^2(\theta_{\alpha,\beta})\le 4\) which is an integer by assumption. Thus, we can list all the possibilities for the angles and for \(\langle \alpha,\beta\rangle\)

If \(\Delta\) is a base for \(\Phi\), then the Cartan matrix associated to \(\Delta\) is \(C=(\langle\alpha_i,\alpha_j \rangle)\in\mathrm{Mat}_{\ell}(\mathbf Z)\) where \(\Delta=\{\alpha_1,\dots,\alpha_{\ell}\}\) where \(\ell=|\Delta|\). Changing the order of roots just permutes the Cartan matrix’s rows and columns.
Definition 5. The Dynkin diagram of a root system \(\Phi\) with respect to a base \(\Delta\) is a graph with undirected or directed edges with possibly multiple edges, such that the vertices are \(\Delta\) and the number of edges between \(\alpha,\beta\in\Delta\) is \(\max(|\langle\alpha,\beta \rangle|,|\langle \beta,\alpha\rangle |)\), directed towards the longer root if the number of edges is more than one.
Obviously the root system is irreducible iff the Dynkin diagram is connected. Two root systems are isomorphic iff they have the same Dynkin diagram. A classification of all Dynkin diagrams can be found here. The bases for the root systems according to these classification can be found here. The simply laced (no multiple edges) Dynkin diagrams shows up in classification problems in many different areas in mathematics: labelled graphs, quivers, 2d conformal field theories, etc. See ADE classification.
The Dynkin diagram also tells us information about the presentation of the Weyl group. For two distinct simple roots \(s,r\in\Delta\), the order \(m\) of \(sr\) in the presentation of the Weyl group is determined by the number of edges between their corresponding vertices in the Dynkin diagram. If there are no edges then \(m=2\), if there is one edge then \(m=3\), if there are two edges then \(m=4\), and if there are three edges then \(m=6\).
Bruhat order on Coxeter groups
An important step in Pawlowski’s paper was bounding \(\mathcal O(v,w)\) using the antichains in the Bruhat order. The Bruhat order can in fact be defined over any Coxeter group.
Definition 6. If \(W\) is a Coxeter group with standard generators \(S\), the Bruhat order on \(W\) is defined by \(u\le v\) iff some substring of a \(S\)-reduced word for \(v\) is a \(S\)-reduced word for \(u\).
As an example, we calculate the Weyl group of the root system arising from \(\mathfrak{sp}_{2n}\) and its Bruhat order. From Example 2.3 earlier, we have \(\Phi=\{\pm e_i\pm e_j:i\ne j\}\cup\{\pm 2e_k:k\}\). To compute the presentation, we first choose a set of simple roots \(\Delta=\{2e_1,e_2-e_1,e_3-e_2,\dots,e_{n}-e_{n-1}\}\), and by computing the Cartan matrix, we derive the following Dynkin diagram which then determines the Weyl group \(W(\Phi)\).
Next, we find the reduced words in the group. For a word in this group, if two neighboring letters differ by an index greater than \(1\) then we cannot reduce the two letters further, and if they do not differ then they reduce to \(1\). Thus the reduced words are the concatonation of proper substrings of \((s_1s_2)^4\) and \((s_ks_{k+1})^3\) for \(k\ge 2\) such that each neighboring pair of such block do not form the string \((s_1s_2)^4\) or \((s_ks_{k+1})^3\) for \(k\ge 2\) and such that the two neighboring ends are not the same letter. For example, the word \(s_3s_4s_3s_4s_5s_4s_5s_7s_6\) is reduced. Observe that the reduced words are unique.

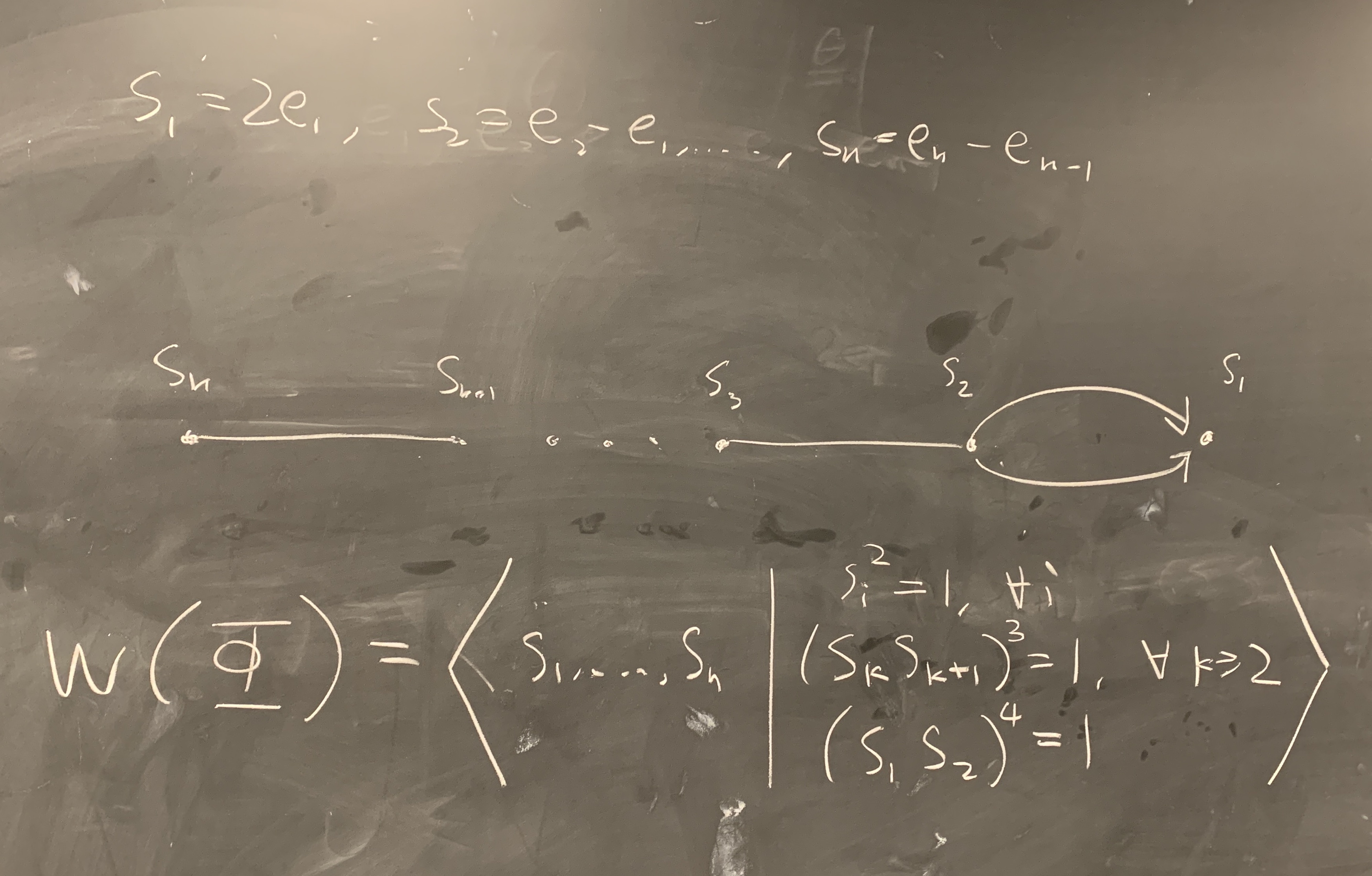
Comments