A Go Variant: Terrain Go

“The rules of go are so elegant, organic, and rigorously logical that if intelligent life forms exist elsewhere in the universe, they almost certainly play go. “

Edward Lasker

The game of Go is an ancient and profound abstract strategy board game that I, albeit losing most of my games, enjoy playing very much. If you have not heard of Go before, see here for a quick guide to the rules of Go. I’ve been recently designing my own variant of Go, which I call “Terrain Go” tentatively for lack of a better name. This variant is inspired by Bobby Fischer’s Fischer random chess, which is a chess variant that, at the outset of the game, randomizes the initial positions of pieces at the players’ home ranks in a certain way that preserves the dynamic nature of the game. The variant is designed to “eliminate the complete dominance of openings preparation in classical chess, replacing it with creativity and talent.” In a similar spirit, we introduce randomness at the outset of Go by way of “terrain”, in a way that preserves the dynamic nature of Go.

Rules

At the beginning of the game, each intersection on the 19 by 19 board will be assigned one of the following types

• Mountain, indicated by a triangle \(\Delta\)
• Water, indicated by a square \(\square\)
• Plains, with no indication

and they are generated randomly in a way such that each group of \(\Delta\) or \(\square\) does not surround empty intersections, and that there are exactly 60 in 2 to 4 groups of each \(\Delta\) or \(\square\), each group having at least 12 stones. Therefore, 60 intersections are mountain, 60 intersections are water, and 240 intersections are plains. In classical Go, with area scoring, each intersection is worth 1 point. However, in Terrain Go, each \(\Delta\) is worth 0 point, each \(\square\) is worth 1.5 points, and each plain is worth 1 point. Additionally, at the beginning, players will take turns placing 3 markings each, called their “forts”, on a “plain” intersection of their choice, which will be indicated by letters. They will each be worth 12 points for the opponent if at the end of the game they end up in the oppoent’s territory (and 0 if it ends up in their own), and once placed, they cannot be captured or removed from the board, or occupied by a stone, or serve as a liberty for another group. Here’s an example of a configuration of the board, where A, B, C are white’s forts, and C, D, E are black’s.

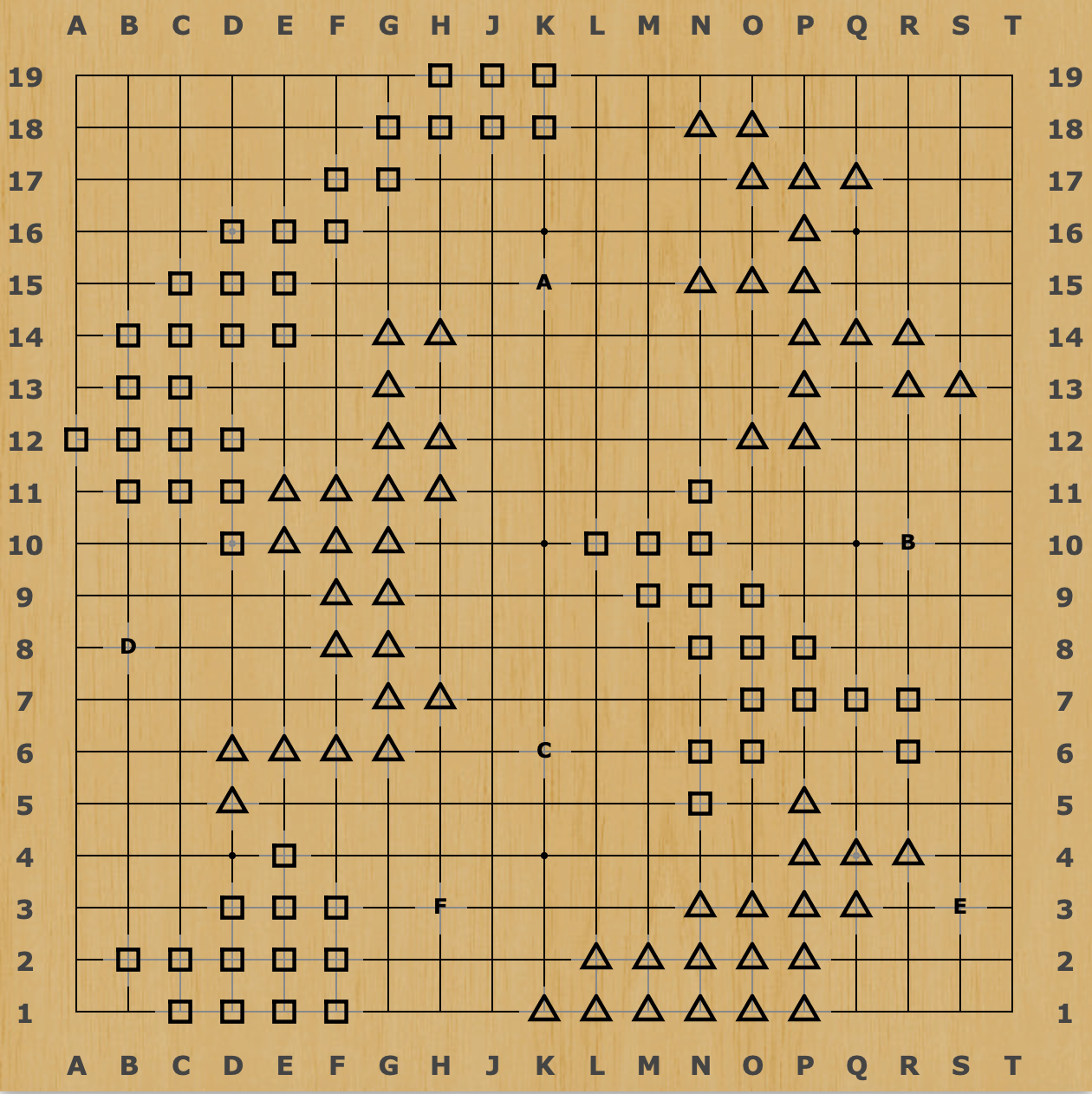
The game will begin with the player who played second in placing the marking, and the rules of capture and Ko, etc, will all follow that of classical Go with the area scoring described above. Additionally, there are special rules for placing stones at moutain or water areas:

1. A stone can only be placed at an intersection marked as \(\Delta\) if it will be a part of a group that has at least 1 liberty outside;
2. a stone can only be placed at an intersection marked as \(\square\) if it will be a part of a group that has at least 1 stone outside.

Since the initial position is randomized, we wouldn’t be able to know the appropriate komi, so the initial positions must be checked by an AI program to make sure it is relatively fair for both players, compensating with a small komi for black or white if necessary.

New Tactics and Strategies

An obvious consequence of the new rules is that any Joseki/Fuseki are rendered obsolete, thus the player cannot obtain any advantage by pre-memorizing openings. The uneven distribution of value of intersections could also lead to interesting strategies. This is arguably closer to real-life war, in which not all areas are of equal strategic value. I would also imagine that it is probably good strategy to start the game around the forts, which are the most valuable positions. In addition, the special rules for placing stones at mountains and waters could lead to novel life and death situations and local tactics. It is more difficult to traverse water because a stone cannot jump in the water alone, it must connect to an existing group that bridges to land. It is even more difficult to traverse mountains since the opponent could try to eliminate outside liberties easily. Therefore, it is possible, for example, to imagine a position where a group of stones is sorrounded “against” a group of mountains or waters. The reader is welcomed to think about more tactics unique to this variant.